8 класс

1. Рассмотрим числа
1-x=1/111111,
1-y=2/222223,
1-z=3/333334,
а также обратные к ним
1/(1-x)=111111,
1/(1-y)=111111+1/2,
1/(1-z)=111111+1/3.
Мы видим, что 1/(1-x) < 1/(1-z) < 1/(1-y).
Поскольку все рассматриваемые числа положительны, 1-x > 1-z > 1-y. Следовательно, x<z<y.

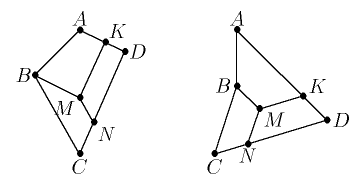
2. Пусть B - наибольший внутренний угол данного четырехугольника ABCD. Проведем разрез BM из вершины B, параллельный стороне AD (точка M попадет внутрь четырехугольника). Из точки M проводим разрезы MN и MK, параллельные сторонам BC и CD соответственно (рис.).

3. Предположим, что ab=cd. Тогда a²+2cd+b²=a²+2ab+b²=(a+b)², c²+2ab+d²=c²+2cd+d²=(c+d)². Таким образом, достаточно найти четыре различных натуральных числа a, b, c и d, для которых ab=cd. Для этого найдем число n, разлагающееся в произведение двух множителей различными способами. Например, таким числом является n=6; в этом случае можно взять a=1, b=6, c=2, d=3.

4. Поскольку 300 и 198 делятся на 6, Петя сможет снять лишь сумму, кратную 6 долларам. Максимальное число, кратное 6 и не превосходящее 500, - это 498.

Докажем, что снять 498 долларов возможно. Произведем следующие операции: 500-300=200, 200+198=398, 398-300=98, 98+198=296, 296+198=494. Сумма, лежащая в банке, уменьшилась на 6 долларов.

Проделав аналогичную процедуру 16 раз, Петя снимет 96 долларов. Затем он может снять 300, положить 198 и снова снять 300. В результате у него будет 498 долларов.

5. Рассмотрим поворот на 180^o по часовой стрелке вокруг центра O (см. рис).

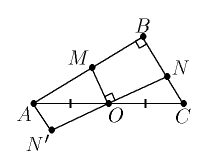
При этом повороте треугольник ONC перейдет в треугольник ON'A. Рассмотрим четырехугольник MAN'O; в нем углы MAN' и MON' прямые. В самом деле, / MAN'=/BAC+/BCA, а/MON'=/MOA+/NOC = 180^o-/MON. Следовательно, MN'²=AM²+AN'²=OM²+ON'². Далее, ON'=ON, OM²+ON²=MN². С другой стороны, AN'=CN, - и требуемое равенство доказано.

1. Произведение чисел на доске не меняется. Действительно, ((a+b)/2)*(2/((1/a)+(1/b))) = ab. Поэтому искомое произведение равно 2.

2. Ответ: да. Приведем стратегию второго игрока. Первые 1000 ходов он пропускает. Ход с номером n>>1000 он делает так:

1) если на n-м и (2000-n)-м местах стоят одинаковые цифры - ничего не делает;

2) если на этих местах - разные цифры, то одна из них не совпадает с той, которая стоит на 1000-м месте. Второй игрок меняет ее с 1000-й цифрой.

3. По теореме об угле между касательной и хордой / CBO = / BAC. С другой стороны, / BAC=/ ACD; следовательно, / CBO =/ OCD. Но / CBO - угол, вписанный в описанную окружность треугольника OBC и опирающийся в этой окружности на дугу OC. При этом / OCD - угол между хордой OC и лучем CD. Следовательно, прямая CD совпадает с прямой, касающейся окружности в точке C.

Замечание. Рассмотренный в задаче параллелограмм обладает следующим свойством: если соединить середины его соседних сторон, то получится параллелограмм, подобный исходному. Для доказательства достаточно заметить, что треугольники BCD и COD подобны.

4. Ответ: k=2.

Обозначим n=1000. Имеем два случая:

1) k>1000. Тогда

       k                       k-(n+1)
      ---                        ---
     /   \             n+1      /   \
1...12...2 - 2...2 = 10   *1...12...2
\        /   \   /         \   /
 --------     ---           ---
    2n        n+1           2n-k

2) k < 1000. Тогда

       k
      ---
     /   \                                     k
1...12...2-2...2 = 1...10...0 - 2...20...0 = 10  (1...1-2...2)
\        / \   /   \   /\   /   \   /\   /        \   / \   /
 --------   ---     ---  ---     ---  ---          ---   ---
    n2      n+1    2n-k   k     n+1-k  k          2n-k   n+1-k

A = 1...1 - 2...2   -
    \   /   \   /
     ---     ---
    2n-2l  n+1-2l

9A = 9...9 - 19...98 = 9...980...01
     \   /    \   /    \   / \   /
      ---      ---      ---   ---
     2n-2l    n-2l      n-2   n-2l

           2n-2l                                 n-2l+1
B - 9A = 10      - 9 9...980...01 = 19...9 = 2*10       - 1
                     \   / \   /     \   /
                      ---   ---       ---
                      n-2   n-2l     n-2l+1

5. Будем считать, что R лежит на AC, S - на BC. Тогда

RQ=RC-QC = (b/2) - ((a+b-c)/2) = ((c-a)/2).
Поскольку треугольники AQP и RQT подобны, а треугольник AQP равнобедренный, то RQ=RT. Следовательно,

ST = RS-RT = RS-RQ= (c/2) - ((c-a)/2) = (a/2) = BS.
Отсюда треугольник TSB равнобедренный и
/SBT =/STB=/ TBA, а BT - биссектриса угла B треугольника ABC.

6.

а) Решение по индукции. База очевидна: один победитель единственного соревнования из двоих - это уже половина. Пусть есть пример n соревнований для 2ⁿ спортсменов с 2^n-1 возможными победителями. Докажем тогда, что есть и (n+1) соревнований для 2ⁿ⁺¹ спортсменов с 2ⁿ возможными победителями. Разделим спортсменов на равные две группы A и A'. Будем считать, что в некотором виде соревнований a любой из A' сильнее любого из A, а в остальных видах - наоборот. Если первым соревнованием провести a, то останется группа A', если любое другое - останется группа A. Применяя индуктивное предположение к группам A и A' по отдельности, получаем пример с 2^n-1+2^n-1=2ⁿ возможными победителями.

б) Укажем для каждого вида соревнований спортсмена, который при любом порядке проведения соревнований выбывает в этом виде или раньше. Построение индуктивное.

Для 1-го вида соревнований - это самый слабый в 1-м виде.

Пусть уже построено множество A^k={a₁, ..., a_k} спортсменов такое, что a_i выбывает в i-м виде соревнований или раньше.

Обозначим через a_k+1 спортсмена, который в (k+1)-м виде слабее всех, не входящих в множество A_k. Докажем, что a_k+1 выбывает в (k+1)-м виде соревнования или раньше при любом порядке соревнований. Пусть после (k+1)-й вид соревнований проходит r-м по порядку, а из множества A_k за первые (r-1) соревнований выбыло w человек. В r-м по порядку виде соревнований выбывает 2^n-r человек. Поэтому a_k+1 проходит в следующее соревнование только при выполнении условия 2^n-r < k-w. Но после (k+1)-го вида соревнований должно пройти по крайней мере k-w соревнований с номерами 1, ..., k. Поэтому k-w < n-r-1 < 2^n-r. Таким образом a_k+1 выбывает в (k+1)-виде соревнований или раньше.

в) Обратим внимание на то, что в конструкции, описанной в пункте а), есть произвол в выборе соревнования, отбирающего группу A. Максимальное число возможных победителей из 2ⁿ спортсменов, соревнующихся в каких-то n видах соревнований из (n+1)-го возможного, равно 2ⁿ-1.

Легче доказать по индукции более сильное утверждение: для всех n>1 существует такой пример (n+1) соревнований с 2ⁿ участниками, что, выбирая n соревнований и порядок их проведения, можно сделать победителями 2ⁿ-1 участников, а единственному исключительному участнику (будем называть его аутсайдером) можно обеспечить выход в финал.

База при n=1 очевидна (два соревнования, в каждом из которых сила спортсменов одинакова).

Индуктивный переход. Строим пример (n+2) соревнований с 2ⁿ⁺¹ участниками, предполагая известным пример для (n+1) соревнований и 2ⁿ участников. Опять разделим спортсменов на равные две группы B и B'. Будем считать, что в некотором виде соревнований b любой из B' сильнее любого из B, а в остальных видах - наоборот. Каждая из групп по отдельности в видах соревнований, отличных от b дает пример выполнения доказываемого утверждения. Дополнительно предположим, что аутсайдер в B - самый сильный среди B в виде b.

Проводя первым b, получим 2ⁿ-1 возможных победителей из B', причем при некотором порядке аутсайдер из B' выйдет в финал по индуктивному предположению.

Если вообще не проводить b, то в первом соревновании выбывают все из B', а далее проводится n-1 соревнование. По индуктивному предположению, выбором первого соревнования и порядка проведения остальных можно сделать победителями 2ⁿ-1 спортсменов из B.

Осталось объяснить, как сделать победителем аутсайдера в B. Для этого первым проводим тот вид соревнований, который является финальным при порядке, обеспечивающем выход аутсайдера в финал. После этого останутся только спортсмены из B. Далее проводим соревнования в таком порядке, который обеспечивает выход аутсайдера из B в финал, а завершаем - соревнованием b. В нем аутсайдер побеждает по построению примера.

1. Рассмотрим квадратный трехчлен f(x)=x²+bx+ac. Из условия следует, что f(c) = c²+bc+ac = (a+b+c)c>0. В точке c функция f(x) принимает отрицательное значение, следовательно, парабола y=f(x) пересекает ось Ox в двух точках, т.е. имеет два различных корня. Значит, дискриминант этого квадратного трехчлена положителен: b²-4ac>0.

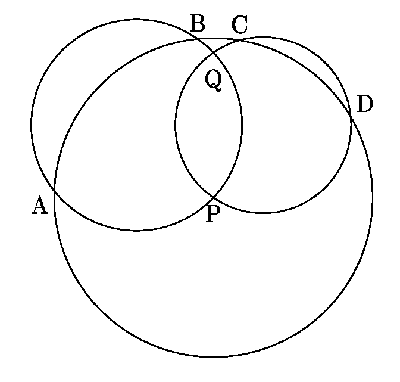
2. Треугольники APB и DPC равнобедренные. Обозначим углы при их основаниях /ABP=/BAP=a, /DCP=/CDP=b. Четырехугольники ABQP и DCQP вписанные, отсюда /AQP=/ABP=a и /DQP=/DCP=b. Получаем: /AQD=/AQP+/DQP=a+b. Далее, /BQP=p-/BAP=p-a, также /CQP=p-b и /BQC=2p-/BQP-/CQP=a+b.

3. Ответ: (1,1).

Докажем вначале, что x и y взаимно просты. Предположим противное. Тогда x и y делятся на некоторое простое число p; пусть p входит в разложения на простые множители чисел x и y соответственно в степенях a>1 и b>1, положим для определенности a>b. Тогда максимальная степень p, на которую делится x³+y, равна b (поскольку x³ делится на p^3a} и тем более на p^b+1, а y делится на p^b и не делится на p^b+1). Но x²+y² делится на p^2b, следовательно, x³+y не может делиться на x²+y². Это противоречие доказывает, что x и y взаимно просты.

Далее, из условия следует, что число x(x²+y²)-(x³+y)=y(xy-1) делится на x²+y². Заметим, что y и x²+y²не имеют общего множителя, большего 1 (т. к. x и y взаимно просты), значит, xy-1 делится на x²+y². Но если xy>1, то это невозможно, т. к. x²+y² > 2xy > xy-1.

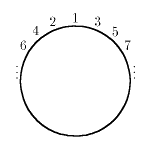
4. Условимся называть красными числа, стоящие в красных секторах, и синими - стоящие в синих секторах. Расстоянием между двумя числами a и b назовем количество чисел, расположенных на меньшей дуге между числами a и b. Числа, расставленные по окружности, разбиваются на пары равных. Выберем ту пару равных чисел, расстояние между которыми наименьшее (если таких пар несколько, выберем любую из них). Пусть для определенности выбранная пара - красная единица и синяя единица, причем меньшая дуга w между ними идет от красной единицы к синей против часовой стрелки. На дуге w либо нет чисел (т. е. две единицы стоят рядом), либо все числа одного цвета, иначе красное и синее числа n были бы на расстоянии меньшем, чем расстояние между единицами. Пусть все числа на этой дуге (если они есть) --- синие (случай, когда они красные, аналогичен). Проведем диаметр, отделяющий синюю единицу от числа, следующего за ним по часовой стрелке; покажем, что этот диаметр искомый. Действительно, рассмотрим полукруг, содержащий синюю единицу. Прочтем синие числа, записанные в этом полукруге начиная с единицы против часовой стрелки - это числа 1, 2, ..., l (l - некоторое число). Прочтем теперь красные числа. Поскольку на дуге w нет красных чисел, то это будут числа n, n-1, ..., n-m (m - некоторое число). Т. к. всего в полукруге n чисел, то в нем записаны все числа от 1 до n по одному разу.

5. Пусть f:[0;1] --> [0;1], f(x)=x/3^1/2 и g: [0;1] --> [0;1], g(x)=1-((1-x))/3^1/2 - функции, отвечающие прыжкам кузнечика. Область значений f - отрезок [0;1/3^1/2], область значений g - отрезок [1-(1/3^1/2);1]. Каждый из этих отрезков имеет длину 1/3^1/2, и вместе они покрывают отрезок [0;1].

Пусть n - некоторое натуральное число. Рассмотрим всевозможные функции h₁ (h₂ (...(h_n(x))...)): [0;1] --> [0;1], где каждая функция h_i - либо f, либо g. Легко видеть, что область значений каждой из этих функций есть отрезок длины (1/3^1/2)ⁿ . Докажем индукцией по n, что эти отрезки покрывают отрезок [0;1]. Для n=1 это утверждение уже проверено. Предположим, что области значений всевозможных функций h₁ (h₂ (...(h_k-1(x))...)) покрывают отрезок [0;1]. Фиксируем любую из функций h₁ (h₂ (...(h_k-1(x))...)). Область значений этой функции покрывается областями значений функций h₁ (h₂ (...(h_k-1(f(x)))...)) и h₁ (h₂ (...(h_k-1(g(x)))...)). Тем самым утверждение доказано.

Пусть теперь на отрезке [0;1] выбрана точка a. Рассмотрим интервал (a-0,01; a+0,01) и покажем, что кузнечик сможет в него попасть. Выберем n столь большим, чтобы было выполнено неравенство (1/3^1/2)ⁿ < 0,01. По доказанному, можно выбрать функцию h₁ (h₂ (...(h_n(x))...)) такую, что точка a принадлежит области ее значений. Тогда вся область значений рассматриваемой функции (отрезок длины (1/3^1/2)ⁿ ) лежит внутри интервала (a-0,01;a+0,01). Это означает, что из любой точки отрезка [0;1] кузнечик попадет внутрь интервала (a-0,01;a+0,01), выполнив последовательно прыжки, соответствующие функциям h_n, h_n-1, ..., h₁ .

6. Ответ: искомая расстановка на рисунке 4 (или получается из нее поворотом либо осевой симметрией).

Лемма. Пусть по окружности расставлены 1999 различных положительных чисел a₁, a₂, ..., a₁₉₉₉ и пусть a₁ > a₁₉₉₈. Рассмотрим следующую операцию: числа a_i и a_1999-i, где i=1, 2, ..., 999, меняем местами, если a_i < a_1999-i, и не меняем в противном случае. Если хотя бы одна пара чисел поменялась местами, то сумма произведений десяток чисел, идущих подряд, увеличилась.

Доказательство леммы. Рассмотрим симметричные группы по 10 чисел a_i, ..., a_i+9 и a_1999-i, ..., a_1990-i. Пусть z - произведение чисел, содержащихся одновременно и в первой, и во второй группе (произведение нулевого числа сомножителей считается равным единице); x и x' - произведения чисел, содержащихся соответственно только в первой и только во второй группе, оставшихся на своем месте после проведения операции; y и y' --- произведения чисел, содержащихся соответственно только в первой и только во второй группе, поменявшихся местами в результате операции. Тогда сумма произведений чисел в рассматриваемых двух группах до операции равна s₁ = zxy+zx'y', а после операции s₂ =zxy'+zx'y. Имеем: s₁-s₂ = z(x-x')(y-y'). Нетрудно видеть, что эта разность неположительна. Кроме того, если в результате операции не все числа остались на своих местах, то хотя бы для одной пары симметричных групп из 10 чисел эта разность строго отрицательна, что и доказывает лемму.

Решение задачи. Считаем числа 1, 2, ..., 1999 расставленными так, что дуги между соседними числами равны. Пусть числа расставлены оптимальным образом, т. е. так, что сумма произведений десяток соседних чисел максимальна. Проведем диаметр через одно из чисел. Из леммы следует, что для всех пар чисел, симметричных относительно этого диаметра, меньшие числа расположены на одной полуокружности, а большие - на другой. С точностью до поворотов и осевых симметрий существует единственная расстановка чисел, удовлетворяющая этому свойству. Действительно, число 2 должно быть рядом с числом 1. Иначе найдется диаметр, отделяющий 2 от 1, причем числа 1 и 2 не симметричны относительно этого диаметра. Обозначим числа, симметричные числам 1 и 2 относительно этого диаметра, соответственно через A и B. Тогда A>1 и 2<B, что противоречит лемме.

1. Ввиду неравенства треугольника a² > (b-c)² . Отсюда a²+2bc > b² + c² . Правая часть положительна, и на нее можно разделить. Получаем, что первое слагаемое в левой части доказываемого неравенства больше 1. То же верно для двух других. Поэтому их сумма больше 3.

2.

а) Достаточно провести прямую через середину дуги и середину ломаной BAC.

б) Пусть A - вершина угла, B и C - концы дуги, D - ее середина. Сегменты, опирающиеся на хорды BD и DC, равны. Поэтому достаточно провести через точку D прямую, которая делит пополам площадь четырехугольника ABDC.

Проведем через середину диагонали BD прямую l, параллельную AC. Пусть, для определенности, l пересекает отрезок AB (случай пересечения l с отрезком AD рассматривается аналогично). Пусть E - точка пересечения l и AB; прямая CE - искомая. Это видно из рассмотрения площадей треугольников ACD, ACE и ACB (с общим основанием AC).

3. Плоскости, которым принадлежат грани каждого цвета, образуют равные правильные тетраэдры. Утверждение задачи следует из того, что сумма расстояний от внутренней точки правильного тетраэдра до его граней постоянна и равна утроенному объему тетраэдра, деленному на площадь грани. (Чтобы доказать это, соединим точку с вершинами правильного тетраэдра и рассмотрим объемы образовавшихся частей, основаниями которых являются грани исходного тетраэдра.)

4. Нужно доказать следующее утверждение. Пусть каждая сторона квадрата имеет длину 1 и разделена на 2ⁿ равных частей (n > 0), а через точки деления проведены прямые, параллельные сторонам. Тогда кузнечик сможет попасть в любую из 4ⁿ полученных клеток.

При n=0 факт тривиален. Проведем индуктивный переход от n к n+1. Рассмотрим какую-то из клеток размера 4^-n-1.Выберем самую близкую к ней вершину исходного квадрата и выполним гомотетию с центром в этой вершине и с коэффициентом 2. Тогда выбранная клетка перейдет в одну из клеток размера 4^-n. По предположению индукции, кузнечик может в нее попасть. Если он прыгнет теперь на половину расстояния до указанной вершины, то он попадет в нужную клетку.

5. Цвета, в которые покрашен граф, занумеруем от 1 до k. Те вершины цвета 2, которые не соседствуют ни с какими вершинами цвета 1, перекрасим в цвет 1. Новая раскраска будет правильной, поэтому в ней k цветов. Значит, какие-то вершины цвета 2 не перекрашены и потому соседствуют с вершинами цвета 1. Аналогично, вершины цвета 3, которые не соседствуют с вершинами цвета 2, перекрасим в цвет 2, и т. д. вплоть до последнего цвета.

После этого рассмотрим какую-либо вершину цвета k. Она не перекрашена, и потому соседствует с вершиной цвета k-1. Эта вершина тоже не перекрашена, так как иначе ее первоначальный цвет был бы k, и она не могла бы соседствовать с вершиной того же цвета. Раз вершина не перекрашена, то она соседствует с вершиной цвета k-2, и т. д. Продолжая этот процесс, построим путь из вершин k цветов, которые не были перекрашены.

6. Единственное решение уравнения: n=2, k=1, l=2, m=3. Докажем это.

Пусть p - простой множитель l. Поскольку n^m=(1+n^k)^l-1, то n^m делится на (1+n^k)^p-1. Но это выражение равно n^k*p+n^2k*p(p-1)/2+n^3k*r, где r - неотрицательное целое число. Разделив на n^k, получим p+n^k*p(p-1)/2+n^2k*r. Если n не делится на p, то это выражение взаимно просто с n, и n^m не может на него делиться. Значит, p - делитель n. Тогда 1+n^k*(p-1)/2+(n^2k/p)*r - натуральное число, большее единицы. Если k>1 или p нечетно, то второе слагаемое делится на n (третье делится всегда), сумма взаимно проста с n, и n^m не может на нее делиться. Следовательно, k=1 и l имеет вид 2^s.

Вспомним теперь, что n^m=(1+n^k)^l-1=(1+n)^l-1= ln + ... В правой части все члены, начиная со второго, делятся на n² . Из этого, поскольку m > 1, следует, что l делится на n. Значит, n, как и l, является степенью двойки. Но
(1+n)^l-1=[(1+n)^l/2+1] * [(1+n)^l/2-1] =
=[(1+n)^l/2+1] ... (n+2)n,} откуда n+2 также является степенью двойки. Следовательно, n=2. Множитель разложения, предшествующий n+2=4, равнялся бы 3² +1=10 и не был бы степенью двойки. Значит, l=2, откуда m=3.

7. Рассмотрим окружность длины 1 как отрезок [0;1] с отождествленными концами. Тогда дробную часть f числа k*lg2 можно рассматривать как точку этой окружности. Первая цифра числа 2^k управляется положением f относительно точек деления 0, lg 2, ..., lg 9. (Например, если 2^k начинается с 7, то 7*10^s<2^k<8*10^s для натурального s. Дробная часть числа k*lg 2 равна k*lg 2 - s, и она находится между lg 7 и lg 8.)

Предположим, что первые цифры чисел 2²ⁿ повторяются с периодом k. Тогда при любом n дробные части чисел 2ⁿ*lg 2 и 2^n+k*lg 2 попадают в один и тот же интервал окружности; длина любого из этих интервалов не превосходит lg 2 < 1/3.

Пусть на окружности отложены дробные части двух положительных чисел A и B; эти дробные части различны и не являются диаметрально удаленными точками окружности; длина меньшей из двух дуг, на которые эти точки делят окружность, равна x. Тогда, как легко показать непосредственно, длина одной из дуг, соединяющих дробные части чисел 2A и 2B, равна 2x. Пусть теперь дробные части чисел A и B лежат в одном интервале; рассмотрим пары 2A и 2B, 4A и 4B и т. д. Из сказанного выше следует, что на некотором шаге одна из дуг, соединяющих дробные части пары, станет больше 1/3, но меньше 2/3. Значит, эти дробные части принадлежат разным интервалам окружности. Применяя эти рассуждения к числам A=2^n₀*lg 2 и B= 2^n₀+k*lg 2, где n₀ - некоторое фиксированное натуральное число, получаем противоречие с предположением о периодичности.