Написав свою программу в текстовый файл с именем, например, prog1.lp, запустите
для вывода результата на экран: lp_solve -S3 < prog1.lp
для сохранения оных в файл: lp_solve -S3 < prog1.lp > res1.txt

1. При запуске из TotalCommander полезно нажимать Shift-Enter.
Вариант — запускать из командной строки cmd.
2. Для диагностики ошибок бывает удобнее выводить результат на экран.
3. При запуске вне класса полезно убедиться, что доступна программа lp_solve
3*. Вот коллекция дистрибутивов lp_solve и фирменного описания для разных операционных систем (там же можно сыскать среду разработки: LPSolve IDE for Windows).
4. Рекомендованное чтение:
Р. Серон, Введение в линейную оптимизацию, Часть 1, Часть 2, Часть 3;
A.C. Bartlett, A.N. Langville, An Integer Programming Model for the Sudoku Problem. Eng PDF;
В.Н.Шевченко, Н.Ю.Золотых, Линейное и целочисленное программирование. Rus PDF.

В конце этого текста приведено несколько комментариев по синтаксису этого языка .

1. Задача о фермере

У фермера есть поле площадью 75 гектаров, на котором он хочет посеять кукурузу и подсолнухи:
Площадь поля: K + П ≤ 75;

Доход от выращивания кукрузы составляет 5 тыс. руб. / га,
подсолнухов – 15 тыс. руб. / га:
Доход: 5 K + 15 П;

Фермер хочет получить максимальный доход. Казалось бы, стоит засеять всё поле кукурузой.
Но возможности хранения урожая ограничены:
Склад: K + 5 П ≤ 300;

• Найдите максимально возможный доход фермера и оптимальную площадь посадок для кукурузы и подсолнухов.
  Решите задачу графически (например, в эл.таблицах) и с помощью lp_solve.
• Насколько может увелиться доход фермера
  ○ при увеличении ёмкости склада на 1?
  ○ при увеличении площади поля на 1?
  ○ при одновременном увеличении площади поля на 1 и ёмкости склада на 1? – есть ли аддитивность?

• Как это повлияет на оптимальный план посадок и на максимальный возможный доход?
  Изобразите грaфически (например, в эл.таблицах) и найдите решение c помощью lp_solve.
• Пусть у фермера есть возможность взять кредит в банке.
  ○ Найдите объём кредита, который имеет смысл брать.
  ○ При какой максимальной стоимости привлечения кредита всё ещё имеет смысл им пользоваться?
  

2. Задача о почтовом отделении

Почтовому отделению требуется различное количество служащих в разные дни недели. Каждый сотрудник работает 5 дней подряд и затем два дня отдыхает.

• День 1 (Понедельник): требуется не менее 17 служащих
• День 2: требуется не менее 13 служащих
• День 3: требуется не менее 15 служащих
• День 4: требуется не менее 19 служащих
• День 5: требуется не менее 14 служащих
• День 6: требуется не менее 16 служащих
• День 7 (Воскресенье): требуется не менее 11 служащих

• Как объяснить lp_solve, что число людей – переменная целочисленная?
• Найдите, какое минимальное количество служащих нужно нанять.
• Во сколько раз желание людей работать 5 дней подряд увеличивает необходимое количество служащих почты?
• Для какого предприятия — большого или маленького — ограничения важнее?

3. Целочисленность и округление

• Найдите оптимальное решение, не предполагая, что число столов и стульев целое.
• Найдите целое решение, округлив оптимальное.
• Найдите целое оптимальное решение.
• Изобразите графически (например, в эл.таблицах) все ограничения и решения.

4. Покрытие множества: задача о тренере баскетбольной команды

Как объяснить lp_solve, что какая-то переменная двоичная?

В баскетбольной команде 7 игроков, причём во время игры на поле пятеро.
У игроков есть склонности: играть в защите (З), центре (Ц) и нападении (Н).
Умение игроков действовать в игре измерено по шкале от 1 (плохо) до 3 (отлично).

Игрок	Склонности	Передачи	Броски	Подбор мяча у щита	Защита
1	З	3	3	1	3
2	Ц	2	1	3	2
3	З, Ц	2	3	2	2
4	Ц, H	1	3	3	1
5	З, H	1	3	1	2
6	Ц, H	3	1	2	3
7	З, H	3	2	2	1

Для игры с сильным соперником, тренер планирует состав команды. Цель — максимально усилить игру в защите на этот матч.

• Не менее 3 игроков должны быть склонны играть в защите.
• Не менее 2 игроков должны быть склонны играть в нападении.
• Нужен по крайней мере 1 игрок, склонный играть в центре.
• «Средний балл» 5 игроков по передачам, подборам мяча у щита, игре в защите и броскам должен быть не ниже 2.
• Если в игре участвует игрок 3, то игрок 6 не может играть, и наоборот.
• Если в игре участвует игрок 1, то также должны играть игроки 4 и 5.
• Либо игрок 2, либо игрок 3 должен принимать участие в игре.

5. Судоку как задача целочисленного линейного программирования

• Сформулируйте судоку как оптимизационную задачу линейного программирования.
• Решите следующие cудоку 4х4;
• Как проверить единственность решения?
• Найдите как можно больше решений каждой из задач:
  

  - - - - - * 2 | * * 3 * | * * - - - - - * * | 4 3 * 3 | * * - - - - -

  - - - - - * 2 | 1 * 3 * | * 3 - - - - - * 3 | 3 * * * | * 1 - - - - -

  - - - - - * 2 | * 4 3 * | * * - - - - - * * | 4 * * * | * * - - - - -

6. Жесткие и мягкие ограничения

Соответствие между заданиями и людьми
Список возможных заданий для каждого человека указан на рисунке.

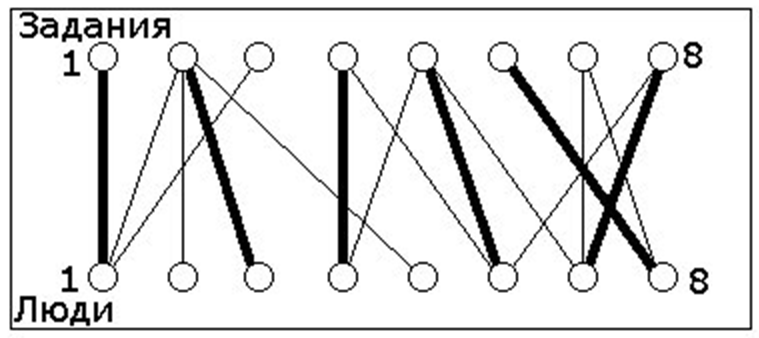
1. Каждый человек может одновременно делать одно задание.
   Каждым заданием может заниматься один человек.
   Найдите разбиение на пары (человек - задание), максимальное по числу пар.
   Сформулируйте и решите задачу линейного программирования.

2. Каждому человеку можно поручить не более двух заданий. Каждым заданием может заниматься один человек.

   а) Каждая пара (человек - задание) увеличивает доход на 1 руб.
   Распределите задания, чтобы был максимальный доход.

   б) Каждое начатое дело увеличивает доход на 1 руб.
   Распределите задания, чтобы был максимальный доход.

   в) Каждый занятый работник увеличивает доход на 1 руб.
   Распределите задания, чтобы был максимальный доход.

   г) А теперь всё вместе:
   Каждая пара (человек - задание) увеличивает доход на 1 руб.
   Каждый бездельник (кто ничем не занят) уменьшает доход на 1 руб.
   Каждое неначатое дело уменьшает доход на 1 руб.
   Распределите задания, чтобы был максимальный доход.
   

3. По-прежнему, каждым заданием может заниматься один человек.
   Каждый человек охотно делает одно дело.
   Если человек занят двумя делами, Вас штрафуют на 0.5 руб.
   Если человек занят тремя делами, Вас штрафуют на 1 руб.
   Каждая пара (человек - задание) увеличивает доход на 1 руб.
   Распределите задания, чтобы был максимальный доход.
   

4. Приведите пример графа, когда штраф меняет
   оптимальное распределение заданий.
   Приведите пример, при какой величине штрафа он превращается в запрет.

5. Работники могут заниматься любым количеством дел.
   Каждое начатое дело увеличивает доход на 1 руб.
   Работники завидуют друг другу, если у них различается количество дел.
   Введите в целевую функцию штраф за модуль разности загрузки двух работников.

Примеры входного файла lp_solve

1. Cначала описывается целевая функция, максимум или минимум которой мы ищем;
   затем — ограничения.
   max: 5 K + 15 P;
   Area: K + P <= 75;
   Sklad: K + 5 P <= 300;
   

2. Переменные объявляют после задания ограничений.
   max: 5 K + 15 P;
   Area: K + P + D <= 75;
   Sklad: K + 5 P <= 300;
   bin D;
   int K, P;
   Последняя строчка сообщает, что переменные K, P целые.
   Предпоследняя — что D может быть только 0 или 1.
   Если не объявлять типа переменной, язык будет считать оную неотрицательным рациональным.

3. Имена неравенств и перемненых начинаются с буквы.
   Имена могут содеджать цифры: A1234 — допустимое имя.

4. Разбор арифметики в lp_solve примитивный:
   Обработки скобок нет;
   Числово перед переменной интерпретируется как множитель;
   Перемножать переменные нельзя.