Пирожок в столовой стоит a рублей и b копеек.
Определите, сколько рублей и копеек нужно заплатить за n пирожков.
Вводятся 3 числа: a, b и n. Все числа целые неотрицательные и не превышают 99.
Необходимо вывести 2 числа — стоимость покупки в рублях и копейках.
| Ввод | Вывод |
|---|---|
10 15 2 |
20 30 |
2 50 4 |
10 0 |
Ваня наблюдает за лягушкой. Изначально она сидит в точке 0 числовой прямой.
Каждую секунду она прыгает на 1 вправо, пока не достигнет точки K.
Затем она начинает каждую секунду прыгать на 1 влево, пока не вернется в точку 0, затем — опять вправо и т.д.
Требуется определить, где окажется лягушка через T секунд.
Вводятся два числа K и T. Оба числа натуральные и не превосходят 1 000 000 000.
Выведите одно число — координату лягушки в момент времени T.
| Ввод | Вывод |
|---|---|
5 8 |
2 |
Необходимо вывести все составные числа от 2 до N, а также их количество.
(Составное число — это натуральное число, которое можно представить в виде произведения двух натуральных чисел, больших 1.)
Вводится натуральное число N, большее 1 и не превосходящее 100.
Выведите все составные числа от 2 до N включительно в порядке возрастания. Затем выведите количество найденных составных чисел.
| Ввод | Вывод |
|---|---|
10 |
4 6 8 9 10 5 |
Даны две сцепленные шестеренки. У одной шестеренки N зубцов, у другой — K. Требуется найти, какое минимальное число поворотов на один зубчик требуется сделать, чтобы шестеренки вернулись в исходное состояние.
Даны два натуральных числа N и K, каждое из которых не превосходящих 10 миллионов.
Выведите искомое количество зубчиков. Гарантируется, что оно не более миллиарда.
| Ввод | Вывод |
|---|---|
2 3 |
6 |
6 21 |
42 |
Во время эксперимента Накодиллы было случайно получено сообщение инопланетян, содержащее формулу вида A + B = C.
Общественности стало интересно, какую же систему счисления используют инопланетяне. Так как внеземная цивилизация была достаточно развита, чтобы отправить межпланетное сообщение, Накодилла предположил, что основание системы счисления довольно мало. Требуется написать программу, которая находит минимальное основание системы счисления, при котором данное равенство выполняется.
В трех строках входных данных содержится три числа A, B и C. Числа состоят из цифр от 0 до 9 и заглавных латинских букв от А до Z.
Требуется вывести единственное число — искомое основание системы счисления. Если такой системы счисления не существует, то вывести -1. Гарантируется, что ответ не превышает 36.
| Ввод | Вывод |
|---|---|
2 2 4 |
5 |
1A 2 20 |
12 |
Будем рассматривать только строчки, состоящие из заглавных латинских букв. Например, рассмотрим строку AAAABCCCCCDDDD. Длина этой строки равна 14. Поскольку строка состоит только из латинских букв, повторяющиеся символы могут быть удалены и заменены числами, определяющими количество повторений. Таким образом, данная строка может быть представлена как 4AB5C4D. Длина такой строки 7. Описанный метод мы назовем упаковкой строки.
Напишите программу, которая берет упакованную строчку и восстанавливает по ней исходную строку.
Вводится одна упакованная строка. В строке могут встречаться только конструкции вида nA, где n — количество повторений символа (целое число от 2 до 99), а A — заглавная латинская буква, либо конструкции вида A, то есть символ без числа, определяющего количество повторений. Максимальная длина строки не превышает 80. Входная строка обязательно заканчивается символом перевода строки.
В выходной файл выведите восстановленную строку. При этом строка должна быть разбита на строчки длиной ровно по 40 символов (за исключением последней, которая может содержать меньше 40 символов).
| Ввод | Вывод |
|---|---|
3A4B7D |
AAABBBBDDDDDDD |
22D7AC18FGD |
DDDDDDDDDDDDDDDDDDDDDDAAAAAAACFFFFFFFFFF FFFFFFFFGD |
По данному натуральному n≤9 треугольник из n строк, в 1-й строке которого все числа от 1 до n, во второй — все числа, кроме последнего, и т.д., в последней — только число 1 (см. пример). Числа должны идти подряд (без пробелов).
| Ввод | Вывод |
|---|---|
3 |
123 |
Вводится число N. Выведите N первых натуральных чисел по следующему правилу: в первой строке одно число, во второй — два, в третьей — три и так далее. В первой строке при этом записано число 1, во второй — 2 и 3, в третьей — 4, 5 и 6 и так далее. В последней строке числа кончаются числом N (их может быть меньше, чем номер строки). Числа в строке должны разделяться пробелом.
| Ввод | Вывод |
|---|---|
6 |
1 |
8 |
1 |
Старинные часы бьют каждые полчаса. Причём в начале каждого часа они бьют столько раз, сколько сейчас часов (по 1 разу — в час ночи и в час дня, по 2 раза — в два часа ночи в два часа дня и т.д., в полночь и в полдень они бьют, соответственно, по 12 раз). И ещё 1 раз они бьют в середине каждого часа.
Дан промежуток времени. Известно, что прошло строго меньше 24 часов (но при этом могли начаться новые сутки). Напишите программу, определяющую, сколько ударов сделали часы за это время.
В первых двух строках вводится начальный момент времени, в следующих двух строках — конечный. Моменты времени задаются двумя целыми числами. Первое число задает часы (от 0 до 23), второе — минуты (от 1 до 59, при этом оно не равно 30).
Выведите одно число — сколько ударов сделали часы за этот отрезок времени.
Примечание. Заметьте, что время в задаче задаётся в 24-часовой форме записи, в то время как часы показывают (и соответственно, бьют) в 12-часовом режиме (т.е., например, в 13 часов часы бьют 1 раз).
| Ввод | Вывод |
|---|---|
5 20 10 25 |
45 |
10 25 5 20 |
135 |
5 2 5 21 |
0 |
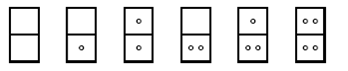
Рассмотрим N-домино. В таком домино каждая костяшка состоит из двух половинок, на каждой из которых нарисовано от 0 до N точек. Полный комплект костяшек такого домино содержит все возможные костяшки, каждую — по одному разу. Например, для N=2 в комплект войдут следующие костяшки: (0,0), (0,1), (0,2), (1,1), (1,2) и (2,2)

Напишите программу, которая по заданному N определит, сколько всего точек изображено на всех костяшках полного комплекта N-домино.
Вводится натуральное число N (1 ≤ N ≤ 30).
Программа должна напечатать одно число — общее количество точек на всех костяшках полного комплекта N-домино.
| Ввод | Вывод |
|---|---|
2 |
12 |
Напомним, что палиндромом называется строка, одинаково читающаяся с обеих сторон. Например, строка abba является палиндромом, а строка abc — нет.
Рассмотрим все натуральные числа, представления которых в десятичной системе счисления являются палиндромами. Необходимо найти N-ое в порядке возрастания такое число.
Вводится одно число N (1 ≤ N ≤ 100000).
Выведите ответ. (Гарантируется, что ответ при указанном ограничении на N не превышает 109.)
| Ввод | Вывод |
|---|---|
1 |
1 |
19 |
101 |
Та же задача, что "Числа-палиндромы – 1", только 1 ≤ N ≤ 109.
При этом гарантируется, что ответ не превышает 1018.
То есть если программа будет делать простой перебор, она будет работать очень долго.