Ранее была задача вычисления числа сочетаний из n элементов по k, для чего необходимо вычисление факториалов трех величин: n, k и n-k. Для этого можно сделать три цикла, что приводит к увеличению размера программы за счет трехкратного повторения похожего кода. Вместо этого лучше сделать одну функцию, вычисляющую факториал любого данного числа n и трижды использовать эту функцию в своей программе. Соответствующая функция может выглядеть так:
def factorial(n):
f = 1
for i in range(2, n + 1):
f *= i
return f
Этот текст должен идти в начале программы, вернее, до того места,
где мы захотим воспользоваться функцией factorial.
Первая строчка этого примера является описанием нашей функции.
factorial — идентификатор, то есть имя нашей функции.
После идентификатора в круглых скобках идет список параметров,
которые получает наша функция. Список состоит из перечисленных через запятую
идентификаторов параметров. В нашем случае список состоит из одной величины n.
В конце строки ставится двоеточие.
Далее идет тело функции, оформленное в виде блока, то есть с отступом.
Внутри функции вычисляется значение факториала числа n
и оно сохраняется в переменной f. Функция завершается инструкцией return f,
которая завершает работу функции и возвращает значение переменной f.
Инструкция return может встречаться в произвольном месте функции, ее исполнение
завершает работу функции и возвращает указанное значение в место вызова.
Если функция не возвращает значения, то инструкция return
используется без возвращаемого значения, также в функциях, не возвращающих значения,
инструкция return может отсутствовать.
Теперь мы можем использовать нашу функцию несколько раз.
В этом примере мы трижды вызываем функцию factorial для вычисления трех факториалов:
factorial(n), factorial(k), factorial(n-k).
n = int(input()) k = int(input()) print(factorial(n) // (factorial(k) * factorial(n - k)))
Мы также можем, например, объявить функцию binomial, которая принимает два целочисленных параметра
n и k и вычисляет число сочетаний из n по k:
def binomial(n, k)
return factorial(n) // (factorial(k) * factorial(n - k))
Тогда в нашей основной программе мы можем вызвать функцию binomial
для нахождения числа сочетаний:
print(binomial(n, k))
Вернемся к задаче нахождения наибольшего из двух или трех чисел. Функцию нахождения максимума из двух чисел можно написать так:
def max(a, b):
if a > b:
return a
else:
return b
Теперь мы можем реализовать функцию max3, находящую максимум трех чисел:
def max3(a, b, c):
return max(max(a, b), c)
Функция max3 дважды вызывает функцию max для двух чисел:
сначала, чтобы найти максимум из a и b, потом чтобы найти максимум из этой
величины и c.
Напишите функцию min4(a, b, c, d), вычисляющую минимум четырех чисел, которая
не содержит инструкции if, а использует стандартную функцию
min. Считайте четыре целых числа и выведите их минимум.
| Ввод | Вывод |
|---|---|
5 |
1 |
Даны четыре действительных числа: x1, y1, x2, y2. Напишите функцию
distance(x1, y1, x2, y2), вычисляющая расстояние
между точкой (x1,y1) и (x2,y2). Считайте четыре действительных числа
и выведите результат работы этой функции.
| Ввод | Вывод |
|---|---|
0 |
1.41421 |
Даны два действительных числа x и y. Проверьте, принадлежит ли точка с координатами
(x,y) заштрихованному квадрату (включая его границу). Если точка принадлежит квадрату, выведите слово YES,
иначе выведите слово NO. На рисунке сетка проведена с шагом 1.

Решение должно содержать функцию IsPointInSquare(x, y),
возвращающую True, если точка принадлежит квадрату и False, если не принадлежит.
Основная программа должна считать координаты точки, вызвать функцию IsPointInSquare
и в зависимости от возвращенного значения вывести на экран необходимое сообщение.
| Ввод | Вывод |
|---|---|
0 |
YES |
3 |
NO |
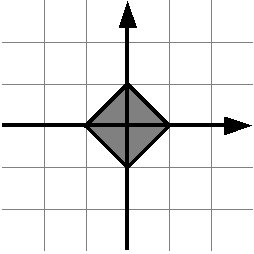
Решите аналогичную задачу для такого квадрата:
| Ввод | Вывод |
|---|---|
0 |
YES |
1 |
NO |
Даны пять действительных чисел: X, Y, Xc, Yc, R. Проверьте, принадлежит ли точка (X,Y) кругу с центром (Xc,Yc) и радиусом R.
Решение оформите в виде функции IsPointInCircle(x, y, xc, yc, r).
| Ввод | Вывод |
|---|---|
0.5 |
YES |
0.5 |
NO |
Проверьте, принадлежит ли точка данной закрашенной области:
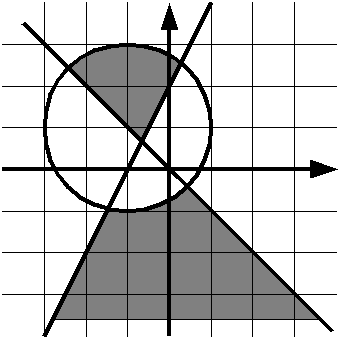
Решение оформите в виде функции IsPointInArea(x, y).
| Ввод | Вывод |
|---|---|
-1 |
YES |
0 |
NO |
Дано действительное положительное число a и целоe число n.
Вычислите an. Решение оформите в виде функции power(a, n).
Стандартной функцией возведения в степень пользоваться нельзя.
| Ввод | Вывод |
|---|---|
2 |
8 |
2 |
0.125 |
Дано натуральное число n>1. Выведите его наименьший делитель, отличный от 1.
Решение оформите в виде функции MinDivisor(n).
| Ввод | Вывод |
|---|---|
4 |
2 |
5 |
5 |
Дано натуральное число n>1. Проверьте, является ли оно простым. Программа должна вывести слово
YES, если число простое и NO, если число составное.
Решение оформите в виде функции IsPrime(n), которая возвращает
True для простых чисел и False для составных чисел.
| Ввод | Вывод |
|---|---|
2 |
YES |
4 |
NO |
Эпиграф:
def ShortStory():
print("У попа была собака, он ее любил.")
print("Она съела кусок мяса, он ее убил,")
print("В землю закопал и надпись написал:")
ShortStory()
Как мы видели выше, функция может вызывать другую функцию. Но функция также может вызывать и саму себя!
Рассмотрим это на примере функции вычисления факториала. Известно, что 0!=1, 1!=1. А как вычислить величину n! для большого n?
Если бы мы могли вычислить величину (n-1)!, то тогда мы легко вычислим n!, поскольку n!=n(n-1)!.
Но как вычислить (n-1)!? Если бы мы вычислили (n-2)!, то мы сможем вычислить и (n-1)!=(n-1)(n-2)!.
А как вычислить (n-2)!? Если бы…
В конце концов, мы дойдем до величины 0!, которая равна 1.
Таким образом, для вычисления факториала мы можем использовать значение факториала для меньшего числа.
(Это можно сделать и в программе на многих других языках программирования, например на C или Pascal.)
def factorial (n):
if n == 0:
return 1
else:
return n * factorial(n - 1)
Подобный приём (вызов функцией самой себя) называется рекурсией, а сама функция называется рекурсивной.
Рекурсивные функции являются мощным механизмом в программировании. К сожалению, они не всегда эффективны (об этом речь пойдет позже). Также часто использование рекурсии приводит к ошибкам, наиболее распространённая из таких ошибок – бесконечная рекурсия, когда цепочка вызовов функций никогда не завершается и продолжается, пока не кончится свободная память в компьютере. Пример бесконечной рекурсии приведён в эпиграфе к этому разделу. Две наиболее распространенные причины для бесконечной рекурсии:
if n == 0, то factorial(0) вызовет factorial(-1),
тот вызовет factorial(-2) и т.д.
factorial(n) будет
вызывать factorial(n), то также получится бесконечная цепочка.
Поэтому при разработке рекурсивной функции важно аккуратно оформлять условия завершения рекурсии и думать, почему рекурсия когда-либо завершит работу.
Дано действительное положительное число a и целое неотрицательное число n.
Вычислите an не используя циклы и стандартную функцию pow, а используя
рекуррентное соотношение an=a * a n-1.
Решение оформите в виде функции power(a, n).
| Ввод | Вывод |
|---|---|
2 |
8 |
Напишите рекурсивную функцию sum(a, b), возвращающую
сумму двух целых неотрицательных чисел. Из всех арифметических операций допускаются
только + 1 и - 1. Также нельзя использовать циклы.
| Ввод | Вывод |
|---|---|
2 |
4 |
Напишите функцию phib(n), которая по данному натуральному n
возвращает n-e число Фибоначчи.
| Ввод | Вывод |
|---|---|
6 |
8 |
По данным числам n и k (0 ≤ k ≤ n) вычислите Сnk. Для решения используйте рекуррентное соотношение Сnk=Сn-1k-1+Сn-1k.
Решение оформите в виде функции C(n, k).
| Ввод | Вывод |
|---|---|
6 3 |
20 |
Дана последовательность чисел, завершающаяся числом 0. Найдите сумму всех этих чисел, не используя цикл.
| Ввод | Вывод |
|---|---|
1 |
17 |
Дана последовательность целых чисел, заканчивающаяся числом 0. Выведите эту последовательность в обратном порядке.
При решении этой задачи нельзя пользоваться массивами и прочими динамическими структурами данных. Рекурсия вам поможет.
| Ввод | Вывод |
|---|---|
1 |
0 3 2 1 |
Возводить в степень можно гораздо быстрее, чем за n умножений! Для этого нужно воспользоваться следующими рекуррентными соотношениями:
an=(a2)n/2 при четном n,
an=a * a n-1 при нечетном n.
Реализуйте алгоритм быстрого возведения в степень. Если вы все сделаете правильно, то сложность вашего алгоритма будет O(log n).
Пользоваться операцией возведения в степень в этой задаче, естественно, нельзя.
| Ввод | Вывод |
|---|---|
1.000000001 |
2.71828 |
Для быстрого вычисления наибольшего общего делителя двух чисел используют алгоритм Евклида. Он построен на следующем соотношении: НОД(a,b)=НОД(a mod b,b).
Реализуйте рекурсивный алгоритм Евклида в виде функции gcd(a, b).
| Ввод | Вывод |
|---|---|
12 |
4 |
Головоломка “Ханойские башни” состоит из трех стержней, пронумерованных числами 1, 2, 3. На стержень 1 надета пирамидка из n дисков различного диаметра в порядке возрастания диаметра. Диски можно перекладывать с одного стержня на другой по одному, при этом диск нельзя класть на диск меньшего диаметра. Необходимо переложить всю пирамидку со стержня 1 на стержень 3 за минимальное число перекладываний.
Напишите программу, которая решает головоломку; для данного числа дисков n
печатает последовательность перекладываний в формате
a b c, где a — номер перекладываемого диска,
b — номер стержня с которого снимается данный диск,
c — номер стержня на который надевается данный диск.
Например, строка 1 2 3 означает перемещение диска номер 1 со стержня
2 на стержень 3. В одной строке печатается одна команда.
Диски пронумерованы числами от 1 до n в порядке возрастания диаметров.
Программа должна вывести минимальный (по количеству произведенных операций) способ перекладывания пирамидки из данного числа дисков.
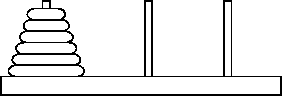
Указание: подумайте, как переложить пирамидку из одного диска? Из двух дисков? Из трех дисков? Из четырех дисков? Пусть мы научились перекладывать пирамидку из n дисков с произвольного стержня на любой другой, как переложить пирамидку из n+1 диска, если можно пользоваться решением для n дисков.
Напишите функцию move (n, x, y),
которая печатает последовательнось перекладываний дисков для перемещения
пирамидки высоты n со стержня номер x
на стержень номер y.
| Ввод | Вывод |
|---|---|
2 |
1 1 2 |
Постановлением ЮНЕСКО оригинал Ханойской башни был подвергнут реставрации. В связи с этим во время пользования головоломкой нельзя было перекладывать кольца с первого стержня сразу на третий и наоборот.
Решите головоломку с учетом этих ограничений. Вам не нужно находить минимальное решение, но количество совершенных перемещений не должно быть больше 200000, при условии, что количество дисков не превосходит 10.
Тесты к этой задаче закрытые.
| Ввод | Вывод |
|---|---|
1 |
1 1 2 |
2 |
1 1 2 |
На дорогах Ханоя было введено одностороннее круговое движение, поэтому теперь диск со стержня 1 можно перекладывать только на стержень 2, со стержня 2 на 3, а со стержня 3 на 1.
Решите головоломку с учетом этих ограничений. Вам не нужно находить минимальное решение, но количество совершенных перемещений не должно быть больше 200000, при условии, что количество дисков не превосходит 10.
| Ввод | Вывод |
|---|---|
1 |
1 1 2 |
2 |
1 1 2 |
В Ханое несправедливо запретили класть самый маленький диск (номер 1) на средний колышек (номер 2).
Решите головоломку с учетом этих ограничений. Вам не нужно находить минимальное решение, но количество совершенных перемещений не должно быть больше 200000, при условии, что количество дисков не превосходит 10.
| Ввод | Вывод |
|---|---|
2 |
1 1 3 |
Первоначально все диски лежат на стержне номер 1. Переместите диски с нечетными номерами на стержень номер 2, а с четными номерами - на стержень номер 3.
Вам не нужно находить минимальное решение, но количество совершенных перемещений не должно быть больше 200000, при условии, что количество дисков не превосходит 10.
| Ввод | Вывод |
|---|---|
2 |
1 1 2 |
3 |
1 1 2 |
Как и в предыдущих задачах, дано три стержня, на первом из которых надето n дисков различного размера. Необходимо их переместить на стержень 3 по следующим правилам:
Самый маленький диск (номер 1) можно в любой момент переложить на любой стержень.
Перемещение диска номер 1 со стержня a на стержень b
будем обозначать 1 a b.
Можно поменять два диска, лежащих на вершине двух стержней, если размеры этих дисков
отличаются на 1. Например, если на вершине стержня с номером a лежит
диск размером 5, а на вершине стержня с номером b лежит диск размером
4, то эти диски можно поменять местами. Такой обмен двух дисков будем обозначать
0 a b (указываются номера стержней, верхние диски которых обмениваются местами).
Для данного числа дисков n, не превосходящего 10, найдите решение головоломки. вам не нужно находить минимальное решение, но количество совершенных перемещений не должно быть больше 200000.
| Ввод | Вывод |
|---|---|
1 |
1 1 3 |
2 |
1 1 3 |