62 Московская математическая олимпиада

8 класс

1. Сравнив дроби 111110/111111, 222221/222223, 333331/333334, расположите их в порядке возрастания.

2. Покажите как любой четырехугольник разрезать на три трапеции (параллелограмм тоже можно считать трапецией).

3. Найдите какие-нибудь четыре попарно различных натуральных числа a, b, c, d, для которых числа a²+2cd+b² и c²+2ab+d² являются полными квадратами.

4. Петин счет в банке содержит 500 долларов. Банк разрешает совершать операции только двух видов: снимать 300 долларов или добавлять 198 долларов.
Какую максимальную сумму Петя может снять со счета, если других денег у него нет?

5. В прямоугольном треугольнике ABC точка O - середина гипотенузы AC. На отрезке AB взята точка M, а на отрезке BC - точка N так, что угол MON - прямой.
Докажите, что AM²+CN²=MN².

1. На доске в лаборатории написаны два числа. Каждый день старший научный сотрудник Петя стирает с доски оба числа и пишет вместо них их среднее арифметическое и среднее гармоническое. Утром первого дня на доске были написаны числа 1 и 2.
Найдите произведение чисел, записанных на доске вечером 1999-го дня. (Средним арифметическим двух чисел a и b называется число (a+b)/2, а средним гармоническим - число 2/((1/a)+(a/b)) ).

2. Двое играют в следующую игру: первый выписывает в ряд по своему желанию буквы А или Б (слева направо, одну за другой; по одной букве за ход), а второй после каждого хода первого меняет местами любые две из выписанных букв или ничего не меняет (это тоже считается ходом). После того, как оба игрока сделают по 1999 ходов, игра заканчивается.
Может ли второй играть так, чтобы при любых действиях первого игрока в результате получился палиндром (т. е. слово, которое читается одинаково слева направо и справа налево)?

3. Диагонали параллелограмма ABCD пересекаются в точке О. Окружность, проходящая через точки A, O, B, касается прямой BC.
Докажите, что окружность, проходящая через точки B, O, C, касается прямой CD.

4. Найдите все такие целые положительные k, что число
1...12...2-2...2
является квадратом целого числа.
(В первом слагаемом (уменьшаемом) всего 2000 цифр, из которых на последних местах стоят цифры "2" в количестве k штук, а остальные цифры - "1";
второе слагаемое (вычитаемое) состоит из 1001 поряд стоящих цифр "2")

5. Вписанная окружность треугольника ABC (AB > BC) касается сторон AB и AC в точках P и Q соответственно, RS - средняя линия, параллельная AB, T - точка пересечения прямых PQ и RS.
Докажите, что T лежит на биссектрисе угла B треугольника.

1. Известно, что (a+b+c)c< 0.
Докажите, что b²>4ac.

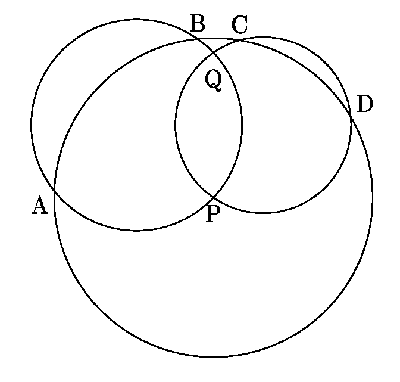
2. Две окружности пересекаются в точках P и Q. Третья окружность с центром в точке P пересекает первую в точках A, B, а вторую - в точках C и D.
Докажите, что углы AQD и BQC равны.

3. Найдите все такие пары натуральных чисел x, y, что числа x³+y и y³+x делятся на x²+y².

4. 2n радиусов разделили круг на 2n равных секторов: n синих и n красных. В синие сектора, начиная с некоторого, подряд записывают против хода часовой стрелки числа от 1 до n. В красные сектора, начиная с некоторого, записываются те же числа и таким же образом, но по ходу часовой стрелки.
Докажите, что найдется полукруг, в котором записаны все числа от 1 до n.

5. Кузнечик прыгает по отрезку [0,1]. За один прыжок он может попасть из точки x либо в точку x/3^1/2, либо в точку x/3^1/2+(1-(1/3^1/2)). На отрезке [0,1] выбрана точка a.
Докажите, что, начиная из любой точки, кузнечик может через несколько прыжков оказаться на расстоянии меньше 1/100 от точки a.

1. a, b, c - стороны треугольника.
Докажите неравенство
((a²+2bc)/(b²+c²))+ ((b²+2ac)/(c²+a²))+ ((c²+2ab)/(a²+b²))>3.

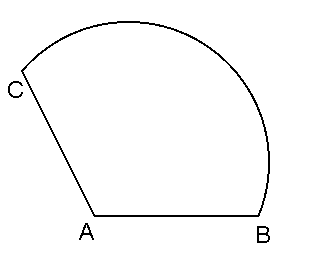
2. Плоская выпуклая фигура ограничена отрезками AB и AC и дугой BC некоторой окружности.
Постройте какую-нибудь прямую, которая делит пополам:
а) периметр этой фигуры;
б) ее площадь.

3. Грани правильного октаэдра раскрашены в белый и черный цвет. При этом любые две грани, имеющие общее ребро, покрашены в разные цвета.
Докажите, что для любой точки внутри октаэдра сумма расстояний до плоскостей белых граней равна сумме расстояний до плоскостей черных граней.

4. На лугу, имеющем форму квадрата, имеется круглая лунка. По лугу прыгает кузнечик. Перед каждым прыжком он выбирает вершину и прыгает по направлению к ней. Длина прыжка равна половине расстояния до этой вершины.
Сможет ли кузнечик попасть в лунку?

5. Граф - это набор вершин, причем некоторые из них соединены ребрами (каждое ребро соединяет ровно две вершины графа). Раскраска вершин графа называется правильной, если вершины одного цвета не соединены ребром. Некоторый граф правильно раскрашен в k цветов, причем его нельзя правильно раскрасить в меньшее число цветов.

Докажите, что в этом графе существует путь, вдоль которого встречаются вершины всех k цветов ровно по одному разу.

6. Решите в натуральных числах уравнение (1+n^k)^l=1+n^m, где l>1.

7. Докажите, что первые цифры чисел вида 2²ⁿ образуют непериодическую последовательность.

Из трех последних задач 11 класса в зачет идут две.

Организационная информация

О результатах олимпиады. Окончательные результаты олимпиады были определены после показа работ и апелляции, которые состоялись 14 марта 1999 года.